Srinivasa Ramanujan was one of India’s greatest mathematicians

Srinivasa Ramanujan was one of India’s greatest mathematicians, known for his extraordinary contributions to mathematical analysis, number theory, infinite series, and continued fractions. His work continues to influence mathematics today, and his life story is an inspiring tale of brilliance, passion, and perseverance.

Early Life:

• Born: December 22, 1887, in Erode, Tamil Nadu, India.
• Parents: K. Srinivasa Iyengar (a clerk in a sari shop) and Komalatammal (a housewife).
• Childhood: Ramanujan showed early signs of exceptional mathematical ability. By the age of 11, he had mastered advanced trigonometry and was working on complex mathematical problems on his own.

Education:

• Ramanujan attended various schools in Tamil Nadu. He excelled in mathematics but struggled in other subjects.
• At the age of 16, he obtained a copy of the book “A Synopsis of Elementary Results in Pure and Applied Mathematics” by G.S. Carr, which influenced his mathematical thinking. He independently developed many complex mathematical concepts after studying this book.
• Despite his brilliance, he failed his college exams due to his lack of interest in non-mathematical subjects, resulting in him losing his scholarship.

Struggles and Early Work:

• After leaving formal education, Ramanujan continued his mathematical work in isolation, producing theories and results independently.
• During this time, he lived in poverty and struggled to find employment. He worked as a clerk to support himself but remained deeply committed to mathematics.

Recognition in India:

• Ramanujan’s work began to attract attention in India after he published his first paper in the Journal of the Indian Mathematical Society in 1911.
• With the help of friends and mentors, he sent some of his work to prominent mathematicians in Europe.

Collaboration with G.H. Hardy:

• In 1913, Ramanujan wrote to G.H. Hardy, a leading British mathematician at Cambridge University. Hardy recognized Ramanujan’s genius despite some skepticism due to the unorthodox nature of his work.
• Hardy invited Ramanujan to Cambridge, where they collaborated from 1914 to 1919. This period was highly productive, resulting in significant mathematical contributions.
• Some of their collaborative work includes the Hardy-Ramanujan asymptotic formula, which relates to the partition of numbers, and the Ramanujan-Hardy number (1729), known as the smallest number expressible as the sum of two cubes in two different ways.

Mathematical Contributions:

• Number Theory: Ramanujan’s work in number theory includes the partition function, which describes the ways a positive integer can be expressed as the sum of positive integers, and his groundbreaking work on modular forms.
• Infinite Series and Continued Fractions: He discovered novel series for π (pi) and made contributions to the field of continued fractions, providing new insights and theorems.
• Mock Theta Functions: Perhaps one of his most profound contributions, these functions have deep implications in number theory and have found applications in modern mathematics, including in string theory and black hole physics.

Return to India and Later Years:

• Ramanujan returned to India in 1919 due to declining health. He continued to work on mathematics even though he was seriously ill.
• Despite receiving recognition from various quarters, including being elected a Fellow of the Royal Society and the first Indian to be elected a Fellow of Trinity College, Cambridge, his life was cut short.

Death:

• Date: April 26, 1920
• Cause: Complications related to tuberculosis and possibly other health issues. He passed away at the young age of 32.

Legacy:

• Ramanujan left behind notebooks filled with thousands of theorems, many of which were proven correct only decades later.
• His life and work have inspired countless mathematicians and have become the subject of various books, plays, and movies.
• Ramanujan’s Legacy in Modern Mathematics: The ongoing work to fully understand and apply Ramanujan’s findings continues today, with the discovery of his work influencing areas as diverse as particle physics and computer science.

Cultural Impact:

• Ramanujan’s story symbolizes the incredible potential of human intellect and the importance of nurturing talent, no matter how unconventional or underprivileged.
• His life has been celebrated in various forms, including the 2015 film “The Man Who Knew Infinity,” starring Dev Patel as Ramanujan and Jeremy Irons as G.H. Hardy.

Honors and Remembrance:

• National Mathematics Day: December 22, his birthday, is celebrated as National Mathematics Day in India.
• Ramanujan Prize: The Ramanujan Prize for young mathematicians from developing countries, awarded annually by the International Centre for Theoretical Physics (ICTP), is named in his honor.
• Statues and Memorials: Statues of Ramanujan have been erected in various educational institutions in India, including at IIT Madras.

Key Takeaways:

• Intuition and Innovation: Ramanujan’s work was driven by intuition, and his results often came without formal proofs, leaving mathematicians the task of verifying them.
• Perseverance: Despite significant challenges, including health issues and a lack of formal education, Ramanujan’s passion for mathematics drove him to make profound contributions to the field.
• Global Influence: His work continues to influence modern mathematics, and his life story inspires scholars and mathematicians worldwide.

The Hardy-Ramanujan asymptotic formula is a significant result in number theory, particularly in the study of partitions of integers. It was discovered by the collaboration between the British mathematician G.H. Hardy and the Indian mathematician Srinivasa Ramanujan.

Background:

• Partition of a Number: In mathematics, a partition of a positive integer nnn is a way of writing nnn as a sum of positive integers, where the order of the addends does not matter. For example, the number 4 can be partitioned in five different ways: 444, 3+13+13+1, 2+22+22+2, 2+1+12+1+12+1+1, and 1+1+1+11+1+1+11+1+1+1.
• Partition Function p(n)p(n)p(n): The partition function p(n)p(n)p(n) gives the number of possible partitions of the integer nnn.

Hardy-Ramanujan Asymptotic Formula:

The Hardy-Ramanujan formula provides an asymptotic expression for the partition function p(n)p(n)p(n) as nnn becomes large. It approximates the value of p(n)p(n)p(n) for large nnn.

The formula is given by:p(n)∼14n3exp⁡(π2n3)p(n) \sim \frac{1}{4n\sqrt{3}} \exp\left(\pi \sqrt{\frac{2n}{3}}\right)p(n)∼4n3​1​exp(π32n​​)

Where:

• p(n)p(n)p(n) is the number of partitions of nnn.
• The symbol ∼\sim∼ indicates that the formula is an asymptotic approximation, meaning it becomes more accurate as nnn increases.
• The expression exp⁡(x)\exp(x)exp(x) is the exponential function, equivalent to exe^xex.

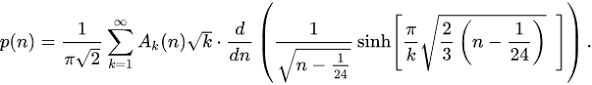
Interpretation:

• The Hardy-Ramanujan formula shows that the partition function grows rapidly as nnn increases.
• The leading term in the exponent, π2n3\pi \sqrt{\frac{2n}{3}}π32n​​, indicates the rapid growth rate of p(n)p(n)p(n).
• The prefactor 14n3\frac{1}{4n\sqrt{3}}4n3​1​ provides a scaling that refines the approximation.

Historical Significance:

• The discovery of the Hardy-Ramanujan asymptotic formula was a groundbreaking achievement in analytic number theory. It was one of the first instances where the circle method was systematically applied to obtain asymptotic results in number theory.
• The formula has profound implications, not just in partition theory but also in various other areas of mathematics, including modular forms and q-series.

Applications and Influence:

• Mathematics: The formula has applications in combinatorics, statistical mechanics, and the study of modular forms.
• Physics: The rapid growth of the partition function as described by the formula is analogous to certain problems in statistical mechanics, particularly in the study of phase transitions.

Example:

For a large integer n=100n = 100n=100, the partition function p(100)p(100)p(100) is exactly 190,569,291. The Hardy-Ramanujan asymptotic formula provides an approximation for this value, showing how it approaches the true value as nnn increases.

The Hardy-Ramanujan formula is a beautiful illustration of how powerful mathematical techniques can yield deep insights into seemingly simple problems like counting partitions of integers.